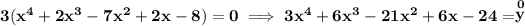since they all have a multiplicity of 1, that simply means they're all there only once, not twice or thrice or more, just once.
now, we have a root of "i", which using a + bi notation, we can simply write as 0 + i.
bearing in mind "complex roots" never come all by their lonesome, their sister is always with them, namely their conjugate is there too, so if
0 + i is here, her sister
0 - i is also a root too.
which means, there are four roots, so the equation is a quartic one, or 4th degree polynomial.
let's also recall that i² = -1.
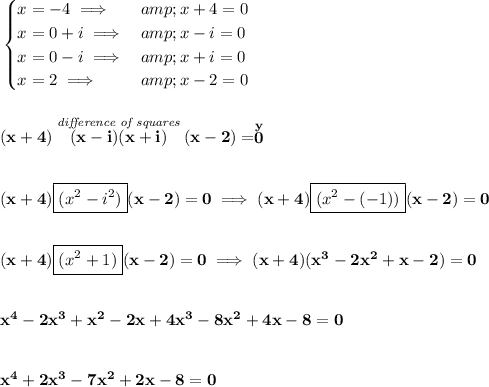
now, since it has a leading coefficient of 3, we simply multiply the whole thing by 3, since usually in the equation to 0, that factor is negligible.