Question

Which second degree polynomial function has a leading coefficient of -1 and root 4 with multiplicity 2

Answer 1

`\bf \stackrel{\textit{root of 4}}{x=4\implies x-4=0}\qquad \stackrel{\stackrel{multiplicity}{of~two}}{(x-4)^2}\qquad \implies \stackrel{FOIL}{x^2-8x+16} \\\\\\ \stackrel{\textit{multiplying by -1}}{-1x^2+8x-16}`

Answer 2

The polynomial is
`-1y^(2)+8y-16`

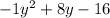
Explanation:

we have to construct a second degree polynomial function has a leading coefficient of -1 that means polynomial having the highest power 2 and having the coefficient of
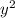`y^(2)` is -1.

One more condition is that having the root 4 with multiplicity 2

Multiplicity means how many times a particular root get when equate to zero or we can say a number is zero for given polynomial function.

`-1y^(2)+8y-16`

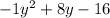
For sol
`-1y^(2)+8y-16=0`

`(y-4)^(2)=0`

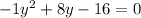
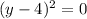
This implies the above polynomial is of multiplicity 2