Question

Given a dilation with the origin O (0, 0), by observation determine the scale factor "K."

Do,K = (6, 12) --->
(3, 6)
1. 1/2
2. 2
3. -3

Answer 1

The correct option is 1. The scale factor is 1/2.

Explanation:

The given rule of dilation is

`D_(o,K):(6,12)\rightarrow (3,6)`

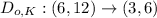
Where, o is origin or center of dilation and K is scale factor.

If a figure is dilation by scale factor K and center of dilation at origin, then

`P(x,y)\rightarrow P'(kx,ky)`

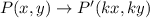
It means

`\text{Scale Factor}=\frac{\text{x-coordinate of image}}{\text{x-coordinate of preimage}}`

`K=(3)/(6)`

`K=(1)/(2)`

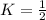
The scale factor is 1/2. Therefore the correct option is 1.

Answer 2

When the dilation is about the origin, the scale factor multiplies every coordinate. That is (considering the x-coordinate) ...
6·k = 3
k = 3/6 = 1/2

The appropriate choice is
1. 1/2