Question

Which of the following functions is not odd?

1) f(x) = sinx
2) f(x) = sin2x
3) f(x) = x³+1
4) f(x) =
`(x)/(x^2+1)`
5) f(x) = ∛(2x)

please explain why 4 and 5 isn't the answer

Answer 1

For odd function f(-x)= -f(x)

1) f(-x)= sin(-x) = -sin(x)=-f(x) sin is odd function
2) f(-x) = sin(-2x) = -sin 2x=-f(x)
3) f(-x)= (-x)³+1 = -x³ +1 (not an odd function)
To be an odd function, it should be like this:
if a function is (x³+1), to be odd f(-x) should be -(x³+1)=-x³-1
4) f(x)= x/(x²+1)
f(-x) = (-x)/((-x)²+1)= -x/(x²+1)=-f(x)
So, f(-x) gives
`- (x)/(x^(2)+1)`,
that means that f(x)= x/(x²+1) is an odd function.
5)f(x) = ∛(2x)

f(-x) = ∛(2*(-x)=∛(2x*(-1)) = ∛(2x)*∛(-1)=- ∛(2x)= -f(x)

Answer 2

Answer: f(x) =x³ + 1 is not an odd function

Explanation:

We are asked about odd functions

If f(x) be a function and f(-x) =-f(x)

then f(x) is an odd function

1) f(x) = sinx

Here f(-x) = sin(-x)

=-sinx sin(-x) = -sinx

Therefore it is an odd function

2) f(x) = sin2x

f(-x) = sin 2(-x)

= sin (-2x)

=-sin2x = -f(x)

Therefore it is an odd function

3) f(x) = x³ +1

f(-x) = (-x)³ + 1

= -x³+1

For odd function it should be -(x³+1)

Hence it is not an odd function

4) f(x) =
`(x)/(x^(2+1) )`

f(-x) =
`(-x)/((-x)^(2) +1)`

=
`(-x)/(x^(2)+1 )`

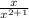
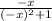
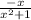
= -f(x)

Therefore it is an odd function

5) f(x) = ∛(2x)

f(-x) =∛(-2x)

= - ∛(2x)

=- f(x)

Hence it is an odd function

∴ 3) f(x) = x³+1 is not an odd function