Answer:
- Domain: [2, ∞)
- Range: [0, ∞)
- Continuity: Function is continuous on its domain [2, ∞).
- Minimum point at (2, 0).
- Increasing function: (2, ∞)
- Symmetry: Neither as there is no symmetry about the y-axis and no origin symmetry.
Explanation:
Given function:
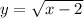
Domain
The domain is the set of all possible input values (x-values).
As the square root of a negative number cannot be taken, the domain of the given function is restricted.
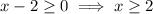
Therefore, the domain of the given function is [2, ∞).
Range
The range is the set of all possible output values (y-values).
As the square root of a negative number cannot be taken, the range of the given function is restricted.
Therefore, the range of the given function is [0, ∞).
Continuity
A function f(x) is continuous when, for every value
 in its domain:
in its domain:
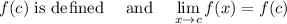
Therefore, the function is continuous on its domain [2, ∞).
Maximums and Minimums
Stationary points occur when the gradient of a graph is zero.
Therefore, to find the x-coordinate(s) of the stationary points of a function, differentiate the function, set it to zero and solve for x.
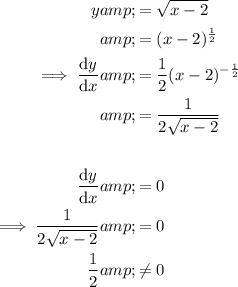
Therefore, there are no stationary points.
As the domain is restricted and f(x) ≥ 0, the minimum point of the function is at point (2, 0).
Increasing/Decreasing Function
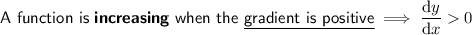

Increasing
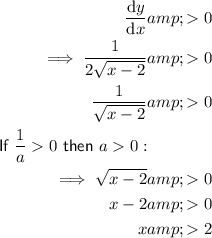
Decreasing
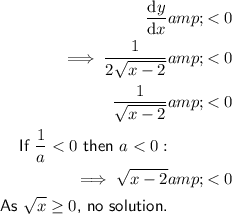
Therefore:
- The function is increasing in the interval (2, ∞).
Symmetry
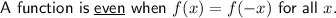

As there is no symmetry about the y-axis (even symmetry) and no origin symmetry (odd symmetry), the symmetry of the function is neither.