For the first one we will use the Law of Sines. First off, though, we need to find angle C's measure. By the Triangle Angle-Sum Theorem, the angles of a triangle all add up to equal 180. Therefore, angle C is 180-15-20 which is 145 degrees. Now we will set up the Law of Sines ratios.
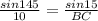
. Solving for BC, we have
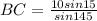
and on our calculators we find that BC is 4.5, last choice above. For the second one, the sin ratio is the side opposite the reference angle over the hypotenuse. The cos ratio is the side adjacent to the reference angle over the hypotenuse. The side opposite angle R is r, and the hypotenuse is q, so the sin R = r/q. For the cos P, the side adjacent to angle P is r, and the hypotenuse is q, so the cos P = r/q. Obviously, those 2 ratios are the same, so your choice is the very first one given.