Question

(BEGINNER LEVEL, Picture provided) Use the line of best fit to predict the total amount of money earned in tips after working 12 hours

Answer 1

It is 110

Slope of the line is 10x So you will earn 110$ in 12 hours.

Answer 2

Option C is correct

$120

Explanation:

The equation of best line is given by:

`y=mx+b` ....[1]

where, y represents the total amount of money earned in tip after x hours, m is the slope and b is the y-intercept.

As per the statement:

From the graph:

Two points are:

(2, 20) and (8, 80)

Formula for slope(m) is given by:

`m = (y_2-y_1)/(x_2-x_1)`

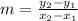
then;

`m = (80-20)/(8-2)=(60)/(6)=10`

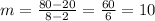
⇒m = 10

Substitute in [1] we have;

`y = 10x+b`

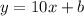
Also , substitute the point (2, 20) to find b;

`20= 10(2)+b`

⇒
`20=20+b`

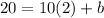
Subtract 20 from both sides we have;

⇒0 = b

or

b = 0

Then, we get the equation:

`y=10x`

We have to find total amount of money earned in tips after working 12 hours.

⇒x = 12 hours

then;

`y=10(12) =120`

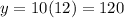
Therefore, the total amount of money earned in tips after working 12 hours is, $120