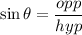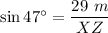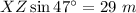Question

HELP! I'm unsure of what this question is actually asking. I solved for side YZ, and found it to be 27.04 m. Is it asking for the length of YZ and XY together or only YZ?

Answer 1

The boy scout was walking on trail YZ from point Y to Z.
Then he decided to go to trail YX. He could have gone back to point Y, made a 90-deg turn and start walking along trail YX. He did not do that.

To go from trail YZ to trail YX, when he got to point Z, he made a 47-deg right turn onto segment XZ which is the short curt between trails YZ and YX.
He walked along ZX until he got onto trail YX at point X. Point X is 29 meters from point Y.

The figure shows angle theta as the 47-degree turn he made.

He walked along the shortcut ZX. When he got to point X, he was on trail YX. The point he got onto trail YX is point X and it is 29 m from point Y.

The question is what is the distance of the shortcut, XZ?

You have a right triangle, XYZ, with legs YX and YZ, and with hypotenuse XZ. You are given one of the acute angles as 47 deg. You are looking for the length of the hypotenuse, XZ.

For the given angle theta, XY is the opposite leg.
XZ is the hypotenuse of the triangle.

The trig ratio that relates the opposite leg to the hypotenuse is the sine.


`\sin \theta = (opp)/(hyp)`


`\sin 47^\circ = (29~m)/(XZ)`


`XZ \sin 47^\circ = 29~m`


`XZ = (29~m)/(\sin 47^\circ)`


`XZ = 39.7~m`