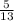2 Answers

Kun · Answer 1 · 2019-12-23T05:59:10+0000

Answer: A.
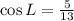
$\cos L=(5)/(13)$

Explanation:

For angle y in a right triangle ,the trigonometric ratio of cos y is given by :-

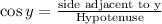
$\cos y=\frac{\text{side adjacent to y}}{\text{Hypotenuse}}$

Given: The side adjacent to angle L= 5 units

The side opposite to angle L = 12 units

Let h be the hypotenuse, then using Pythagoras in the given right triangle, we get

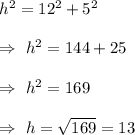
$h^2=12^2+5^2\\\\\Rightarrow\ h^2=144+25\\\\\Rightarrow\ h^2=169\\\\\Rightarrow\ h=√(169)=13$

Thus, hypotenuse = 13 units

Now, the trigonometric ratio for cos L is given by :-

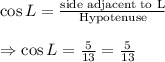
$\cos L=\frac{\text{side adjacent to L}}{\text{Hypotenuse}}\\\\\Rightarrow\cos L=(5)/(13)=(5)/(13)$

Hence, the value of cos L =

Please log in or register to add a comment.