Answer:
The domain of the function is
![D=[x|x\\eq-(5)/(3)]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/46i3z1sauyj7jezk8rviy0qm3lfpzxwd0h.png)
Step-by-step explanation:
Given :
 and
and
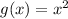
To find :
 and state it's domain?
and state it's domain?
Solution :
The required function is
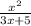
Now, The domain is defined as the set of values of possible value that make function work.
The function to be defined when denominator cannot be zero.
So,
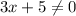
i.e.

Therefore, The domain of the function is
![D=[x|x\\eq-(5)/(3)]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/46i3z1sauyj7jezk8rviy0qm3lfpzxwd0h.png)