If
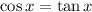
, then
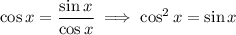
for
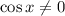
. This is definitely the case, since
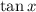
is undefined if
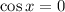
. Now,
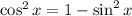
, so we have
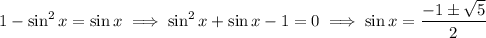
or
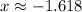
and
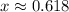
. One of these solutions is larger than 1 in absolute value, but
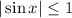
, so we omit that solution, leaving us with
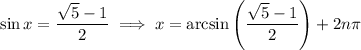
for integers

, which follows from the fact that
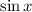
has period
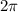
.