Question

Given tan(A) = 2 and A is in Quadrant I, find sin(2A) and find cos(2A).

0
1
1/2
4/5

0
1
1/2
-3/5

Answer 1

We can use following formula


`tan^(2)(A) = (1- cos(2A))/(1+cos(2A)) \\ \\ tan(A) =2, so \\ \\4= (1- cos(2A))/(1+cos(2A)) \\ \\1-cos(2A)=4+4cos(2A) \\ \\ 5cos(2A) = -3 \\ \\ cos (2A) = -3/5`

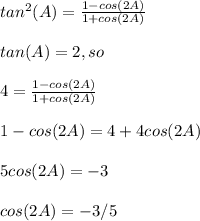
Now, we need to find sin(2A).


`sin^(2)(2A) + cos^(2)(2A) = 1 \\ \\ sin^(2)(2A) + (- (3)/(5))^(2) =1 \\ \\ sin^(2)(2A) =1 - (9)/(25) \\ \\ sin^(2)(2A) = (16)/(25) \\ \\ sin(2A) = (4)/(5) \ or \ - (4)/(5)`

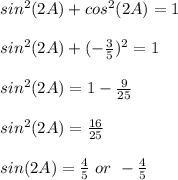
Because, the angle A is in the 1st quadrant, and cos(2A) is negative, that means that the angle 2A is in the 2nd quadrant and sin(2A) is a positive number,so sin(2A) = 4/5.


sin(2A) = 4/5
cos(2A) = -3/5