Question

Please give an explanation? 30 points

Answer 1

The composition of two rotations about the same point (Z) is the sum of the rotations. This can be proved using the matrix versions of the rotations.

This means

`R_z(t1)\circ{R_z(t2)} = R_z(t1+t2)}`
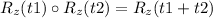
where
R=rotation operator
z=centre of rotation
t1,t2 are angles of rotation
In this particular case, the composition is commutative, i.e. order does not matter because addition of the angles is also commutative.

Thus substituting values, t1=170, t2=100

`R_z(170)\circ{R_z(t2)} = R_z(170+100)}=R_z(270)`

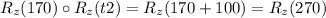
So the result of the composition is a rotation of 270 degrees about Z from the original position, which is also equal to a rotation of -90 degrees.