Answer:
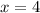

Explanation:
We have been given an image of two congruent circles. We are asked to find the value of x and y for our given circles.
Since
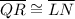 , so
, so
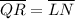 .
.
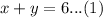
Since
 , so
, so
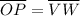 .
.

From equation (1), we will get:
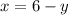
Upon substituting this value in equation (2), we will get:
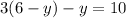
Upon using distributive property, we will get:
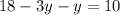
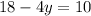
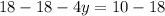



Therefore, the value of y is 2.
Now, we will substitute
 in equation (1) as:
in equation (1) as:
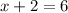
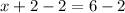
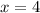
Therefore, the value of x is 4.