Question

Why is the answer B? Plz explain.

Answer 1

The original can be rewritten as
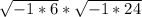
`√(-1*6)* √(-1*24)`. Because i^2 is equal to -1, we can replace the -1 in each radicand with i^2, like this:
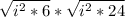
`√(i^2*6)* √(i^2*24)`. Now, i-squared is a perfect square that can be pulled out of each radicand as a single i.
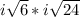
`i √(6)*i √(24)`. 24 has a perfect square hidden in it. 4 * 6 = 24 and 4 is a perfect square. So let's break this up, step by step.
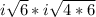
`i √(6)*i √(4*6)` and then
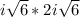
`i √(6)*2i √(6)`. We will now multiply the i and the 2i, and multiply the square root of 6 times the square root of 6:
`2i^2 √(36)`. 36 itself is a perfect square because 6 * 6 = 36. So we will do that simplification now.
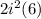
`2i^2(6)`. Multiplying the 2 and the 6 gives us
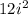
`12i^2`. But here we are back to the fact that i-squared is equal to -1, so 2(-1)(6) = -12. See how that works?

Answer 2

Remark
Any two (or more than 2) square roots when multiplied together can be put under 1 square sign.

In this case sqrt(-6)*sqrt(-24) can be put under 1 square root sign.

sqrt( -6 * - 24) = sqrt(+144) = 12
For this question you do not need to solve the complex numbers.