Hello !
If you mist find the area of the rhombus,you need to calculate the length of the diagonals.
We have the rhombus ABCD.The diagonals are are AC and BD .
Here's a formula to find out the distance between two points in the Cartesian system : (let's take randomly 2 point and their coordinates)
M (m₁,m₂) ; N (n₁,n₂) ⇒ MN = \sqrt{ (m_{1} - n_{1})^{2} + (m_{2} - n_{2})^{2} }
Now it's simple to calculate the diagonals :
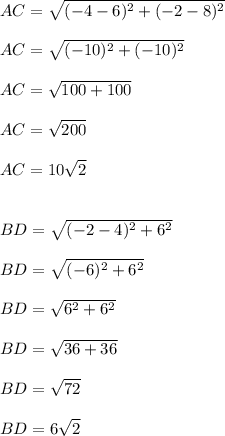
The area is :

Answer: 60 u²
The representation is below.
Have a nice day :)