Question

The product of two positive numbers is 112. One number is 6 more than the other. Determine the two numbers.

Answer 1

The answer is 8 and 14.

Explanation:

Answer 2

Hey there!

Let x equal the smaller positive number and let y equal the greater number.

We can represent the product of the two numbers equaling 112 with this equation:
xy=112

We can represent the larger number being greater than the smaller number by 6 with this equation:
y=x+6

Because you know that the value of y is equal to x+6, you can substitute x=6 for y in the first equation:
y=x+6
xy=112

x(x+6)=112

Now, simplify and set your equation to 0 so the equation can be solved as a quadratic:
x(x+6)=112

`x^(2)`+6x=112

`x^(2)`+6x-112=0

Use the quadratic formula to solve for the values of x:

`\frac{-6+- \sqrt{ 6^(2) -4(-112)(1)} }{2}`

`(-6+- √(36+448) )/(2)`

`(-6+- √(484) )/(2)`

`(-6+-22)/(2)`
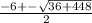
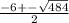
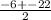
x=8 or -14

Because you want a positive solution, you would use x=8 as one of your final solutions.

Now, you need to find the other number.

To do this, plug x=8 into y=x+6.
y=8+6
y=14

Therefore, your final answers would be 8 and 14.

Hope this helps!