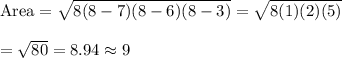Question

Triangle LMN has sides measuring 7 meters and 6 meters and a perimeter of 16 meters.

Heron’s formula: Area = 

What is the area of triangle LMN? Round to the nearest square meter.

3 square meters

9 square meters

28 square meters

34 square meters

Answer 1

third side = 16 - (7 + 6) = 3 m
semiperimeter = 16/2 = 8 m


`Area = √(8(8-7)(8-6)(8-3))= √(8 \cdot1\cdot2\cdot5)= √(80) \approx 9 \ m^2`

Answer: 9 square meters

Answer 2

9 square meters

Explanation:

Heron's formula first tells us how to find the semi-perimeter, S, given sides A, B and C:

`S=(A+B+C)/(2)`

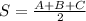
Next we are told how to find the area:

`\text{Area}=√(S(S-A)(S-B)(S-C))`

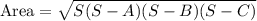
We know that the perimeter, or distance around all three sides, is 16. Letting x represent the unknown side, this gives us

16 = 7+6+x

16 = 13+x

Subtracting 13 from each side, we have

16-13 = 13+x-13

3 = x

Next we find the semi-perimeter:

`S=(7+6+3)/(2)=(16)/(2)=8`

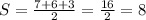
Lastly we use these to find the area:

`\text{Area}=√(8(8-7)(8-6)(8-3))=√(8(1)(2)(5))\\\\=√(80)=8.94\approx 9`