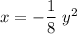Question

Write an equation for a parabola in which the set of all points in the plane are equidistant from the focus and line. F(–2, 0); x = 2

Answer 1

x =
`-(1)/(8)`
`y^(2)`

Explanation:

Answer 2

The line is called the directrix. Here we have a vertical directrix, so a parabola sideways from usual.

Geometry is best done with squared distances. The squared distance from an arbitrary point (x,y) to the vertical line x=2 is
`(x-2)^2.`

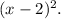
We equate that to the squared distance of (x,y) to the focus (-2,0):


`(x-2)^2 = (x - -2)^2 + (y - 0)^2`


`x^2 -4x + 4=x^2 +4x +4 + y^2`


`-8x = y^2`

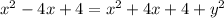
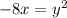
We could call that done. A more standard form might be


`x =- \frac 1 8 \ y^2`