Question

How much would $100 invested at 8% intrest compounded annually be worth after 15 years? round your answer to the nearest cent. do not include units in your answer a(t) = P(1 + r/n)^nt

Answer 1

Our P = 100, r = .08, n = 1 (annually means once a year), and t = 15. Filling in accordingly, we have
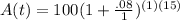
`A(t)=100(1+ (.08)/(1))^((1)(15))`. Simplifying a bit gives us
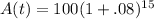
`A(t)=100(1+.08)^(15)` and
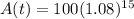
`A(t)=100(1.08)^(15)`. Raising that number inside the parenthesis to the 15th power gives us
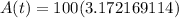
`A(t)=100(3.172169114)`. Multiplying to finish means that A(t) = $317.22