Question

For positive integers $a$, $b$, and $c$, what is the value of the product $abc$? \[ \dfrac {1}{a + \dfrac {1}{b + \dfrac {1}{c}}} = \dfrac38 \]

Answer 1

4

Explanation:

Answer 2

I don't think the $ signs work as math delimiters. I would be nice if they did.

That looks like a simple continued fraction ("simple" is a technical term meaning the numerators are all 1).


`\frac{1}{a + \frac {1}{b + \frac {1}{c}}} = \frac 3 8`

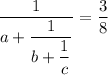
I could go on for hours about continued fractions. The way we expand a regular fraction as a continued fraction is essentially Euclid's algorithm for the GCD:


`(3)/(8) = (1)/(\frac 8 3) = (1)/(2 + \frac 2 3) = (1)/(2 + (1)/(\frac 3 2)) = (1)/(2 + (1)/(1 + \frac 1 2))`

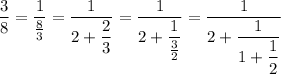
So we have a=2, b=1, c=2, a product

abc=4