To derive the function, we will use the power rule.
Power rule is expressed with the following formula:
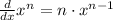
Use this rule to derive both terms in the function:
![(d)/(dx) [6x - x^2] = (d)/(dx) 6x - (d)/(dx) x^2](https://img.qammunity.org/2019/formulas/mathematics/college/3ablj9yf8tist22rd57rzghor7rth1cskf.png)
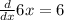
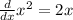
![(d)/(dx) [6x - x^2] = 6 - 2x](https://img.qammunity.org/2019/formulas/mathematics/college/ya0hlwh7e2972hlckba6r2hkx27bfmik7l.png)
We can now plug in the x-value for this derivative to find the slope of the tangent line at said x-value:
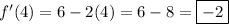
The slope of the tangent line at x = 4 will be
-2.