Question

The equation = 1 represents a hyperbola centered at the origin with a focus of (0,−10).

(y^2/8^2)-(x^2/?^2)=1

The positive value
correctly fills in the blank in the equation.

Answer 1

Focus of parabola(c) = (0,10) and (0,-10).

The given equation of hyperbola is

`(y^2)/(8^2)-(x^2)/(a^2)=1`

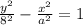
b=8

If the equation of Hyperbola is,

`(y^2)/(b^2)-(x^2)/(a^2)=1`

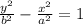
then,
`b^2=a^2(e^2-1)`

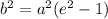
-------------------------(1)

Where , e is the eccentricity of Hyperbola.

c=a e

10= a e

`e=(10)/(a)`

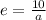
Putting the value of e, in equation (1)

`8^2=a^2[(10)/(a)]^2-1]\\\\ 64=a^2 * (100)/(a^2)-a^2\\\\ a^2=100-64\\\\ a^2=36\\\\ a=\pm 6`

So, the equation of Hyperbola will be

`(y^2)/(8^2)-(6^2)/(a^2)=1`

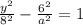
Blank Space = 6

Answer 2

The answer is 6 I just took the test