Question

Solve for x in the equation x^2-10x+25=35.

Answer 1

So, this is too vague but I'll solve for both quadratic formula and find the discriminant.

Quadratic formula: x=5+√35 OR x=5−√35
Finding the discriminant: 141

Answer 2

`x_(1)=5+√(35)`

`x_(2)=5-√(35)`

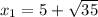
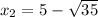
Explanation:

the equation is

`x^2-10x+25=35`

to solve we need to make the equation equal to zero, for that we substract 35 on each side:

`x^2-10x+25-35=0\\x^2-10x-10=0`

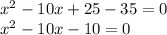
we have now an equation in the general form:
`ax^2+bx+c=0`

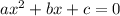
where

`a=1`

`b=-10`

`c=-10`

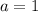
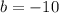
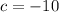
and we find the values for x with the general formula:

`x=(-b+-√(b^2-4ac) )/(2a)`

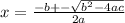
substituting known values

`x=(-(-10)+-√((-10)^2-4(1)(-10)) )/(2(1))\\x=(10+-√(100+40) )/(2)\\x=(10+-√(140) )/(2)\\x=(10+-√(4*35) )/(2)\\x=(10+-2√(35) )/(2)\\x=5+-√(35)`

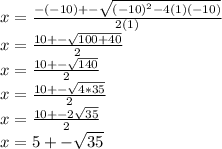
since we had a quadratic equation we will have 2 answers, one taking the positive sign and the other with the negative sign:

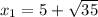`x_(1)=5+√(35)` ≈ 10.916

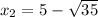`x_(2)=5-√(35)` ≈ -0.916