Question

-7/8 + (-1/2) = in simplest form

Answer 1

To begin to solve this problem, we must first note that when you are doing n + (-z), it is equal to n - z. Now, knowing this, we need to begin to find the LCD of 8 and 2. The LCD of 8 and 2 is 8, so now we need to turn -
`(1)/(2)` into something over 8. -
`(1)/(2)` becomes -
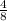
`(4)/(8)`. Now, we can subtract the numerators over a common denominator. -7 - 4 is -11, so -
`(7)/(8)` + (-
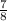
`(1)/(2)`) is -
`(11)/(8)`.

Answer 2

Find a common denominator (in this case 8)

Multiply 4 to both numerator and denominator of -1/2

-1/2(4/4) = - 4/8

-7/8 - 4/8

Simplify. Combine terms

-7/8 - 4/8 = -11/8

Simplify. Change to mixed fraction

-11/8 = -8/8 - 3/8

-1 3/8 is your answer

hope this helps