Not drawn to scale, thanks.
What they're trying to get you to think about with this question is what are the consequences of measurements "correct to the nearest centimeter."
When our numbers are approximations, meaning they're inexact, and we use them in calculations, the things we compute will also be inexact approximations. This problem is trying to get us to understand how inexact an area calculated with inexact numbers can be.
We're interested in the greatest possible area of the shaded region. That will happen when the outer numbers are as big as they can be and the inner white region numbers are as small as they can be because we subtract the white rectangle from the big rectangle to get the shaded area.
If these measurements were exact we'd have a shaded area of
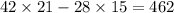
We're allowed to adjust the numbers so that the numbers here are still arguably the nearest centimeter.
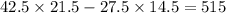
Wow, big difference.
Final answer: 515 square centimeters