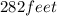Question

Please Help, I also need the work along with the answer.

Suppose that in a rectangular parking lot, if one goes from corner to corner, the distance is 37 yards. The length of the parking lot is 1 yard less than 3 times the width. If a fence is to be built around the lot, how many feet long should the fence be?

Answer 1

1. You have that the diagonal of the rectangle that goes from corner to corner, divides the rectangle into two equal right triangles. Therefore, you can apply the Pythagorean Theorem to solve the problem, as following:

`d^(2) = w^(2)+ l^(2)`

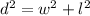
Where
`d` is the diagonal,
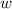`w` is the width and
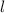`l` is the length.

2. You have that the length is:

`l=3w-1`

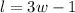
3. The diagonal is:

`d=37 yards`

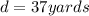
3. Substitute them into the equation and solve for the width:

`37^(2)= w^(2)+ (3w-1)^(2) \\ 10 w^(2) -6w-1368=0 \\ w=12yards`

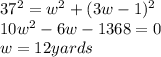
3. Therefore, the length is:

`l=3(12yards)-1=35yards`

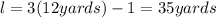
4. The perimeter is:

`P=2(12yards)+2(35yards) \\ P=94yards \\ P=282feet`

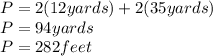
The answer is:
`282feet`