Question

A complex number z = a + bi has an absolute value of 3.28. What could the values of a and b be?

Answer 1

a=1.7 b=2.8 (c)

Answer 2

a could be equal to 1

b could be equal to 3.1238

Step-by-step explanation:

The absolute value of a complex number is calculated as follows:

a + bi =
`√(a^2 + b^2)`

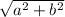
Now, we are given that:

complex number is ............> z = a + bi

absolute vale ..........> 3.28

This means that:

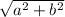`√(a^2 + b^2)` = 3.28

Square both sides:

a² + b² = (3.28)²

a² + b² = 10.7584

Since we have one equation in two unknowns, therefore, we need to assume one of the variables and solve for the other.

Assume a = 1:

1 + b² = 10.7584

b² = 9.7584

either b = 3.1238

or b = -3.1238

Based on the above, one of the possible solutions is:

a = 1

b = 3.1238

You can assume any other value for the a and solve for b.

Hope this helps :)