Question

Find the four rational numbers and irrational numbers between 2/5 and 5/6

Answer 1

The four?

Of course there are an infinite number of rationals between any two different real numbers, as well as an even bigger infinite number of irrationals.

The average will be between the numbers:


`\frac 1 2 (\frac 2 5 + \frac 5 6) = (37)/(60)`

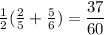
That's a lot of work to get a number in between. We can just see


`\frac 1 2`
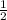
is between the two numbers.

The mediant, or freshman addition, will always be in between:


`(2 + 5)/(5 + 6) = (7)/(11)`

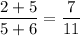
2/5=.4 and 5/6 is about .83, so


`.6 = (6)/(10)`

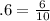
is in between as is .7, .41, .530940394 and as many rationals as we care to generate.

To get irrationals we could just add a teeny irrational to the ones we just generated, like
`(6)/(10) + (\pi)/(100)`

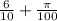
We could just change that denominator a bit and get as many as we like.

But let's get some square roots. The geometric mean will be between


`√( \frac 2 5 \cdot \frac 5 6 ) = (1)/(√(3))`

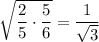
That's the tangent from one of trig's biggest cliches, but I digress. It's in between.

While we're on trig cliches,


`(1)/(√(2))`

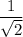
is in between as well.

Keeping with the trig theme, also in between are


`\frac{\pi} 6`

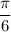
and


`(\pi)/(4)`


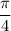
the angles associated with the some of the above trig function values.

We could obviously go on as long as we cared to.