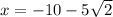Let u = x+2. That makes our equation, in terms of u:
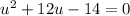
. Fitting this into the quadratic formula looks like this:
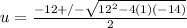
. Simplifying a bit gives us
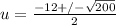
. Simplifying that in terms of the radical gives us
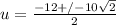
. Reducing that numerator by the 2 in the denominator gives us
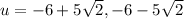
. If u = x + 2, then we make that substitution now to solve for x:
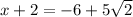
and
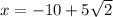
;
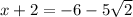
and