Answer : The mass of
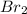 needed are, 131.8 grams
needed are, 131.8 grams
Solution : Given,
Mass of Al = 15 g
Molar mass of Al = 27 g/mole
Molar mass of
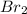 = 159.8 g/mole
= 159.8 g/mole
First we have to calculate the moles of Al.

Now we have to calculate the moles of
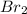
The given balanced reaction will be,
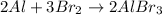
From the balanced reaction, we conclude that
As, 2 moles of Al react with 3 moles of
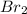
So, 0.55 mole of Al react with
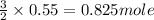 of
of
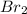
Now we have to calculate the mass of
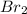
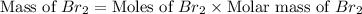
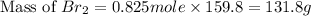
Therefore, the mass of
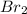 needed are, 131.8 grams
needed are, 131.8 grams