Question

Please Help!!!

Does the following infinite series coverge or diverge?

Explain You're answer?


`(1)/(2) + (2)/(9) + (4)/(27) + (8)/(81) + ...`
A. It Diverges; it does not have A sum

B. It converges; it does not have A sum

C. It Diverges; it has a sum.

D. It converges; it has a sum

Answer 1

B and C are absurd; if a series converges, it must have a sum, but if a series diverges, it cannot have a sum.

Now, notice that


`\frac12+\frac29+\frac4{27}+\frac8{81}+\cdots=\frac12+(2^(2-1))/(3^2)+(2^(3-1))/(3^3)+(2^(4-1))/(3^4)+\cdots`

That is, we can write the sum more compactly as


`\frac12+\frac12\displaystyle\sum_(n=1)^\infty\left(\frac23\right)^n`

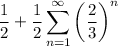
The series is geometric with common ratio
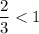
`\frac23<1`, so the series converges (and thereby has a sum), so the answer is D.