Question

The longest side of a polygon exceeds Twice the length of the longest side of a similar polygon by 3. If the ratio of similitude of the polygons is 4:9, find the length of the longest side of each polygon.

Answer 1

Let
length of the longest side of the SMALLER polygon = x
then
length of the longest side of the LARGER polygon = 2x+3

We are given the ratio of similitude is 4:9, which is also the ratio of the sides.

So we equate the ratios and solve for x


`(x)/(2x+3)=(4)/(9)`
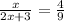
Cross multiply:

`9x=4(2x+3)`
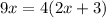
expand by distributing 4 (to both terms in parentheses)

`9x=8x+12)`
subtract 8x from both sides

`9x-8x=12)`

`x=12)`

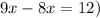
Hence the
longest side of smaller polygon = x = 12 units
longest side of larger polygon = 2x+3 = 2*12+3 = 27 units