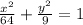If the co-vertices are (0, 3) and (0, -3) where x is 0 and y has a value, then y is the minor axis. That means that the x axis is the major axis. Because of what the co-vertices are, the center of the ellipse is at the origin. The formula for an ellipse that has a horizontal major axis is

. The a value will always be larger than the b value, therefore, the a value goes under the coordinate that is the major axis. Here, its the x-axis. a is the distance that the outer edge of the ellipse is from the center. It's 8 units away from the center along the x axis and 3 units along the y axis from the center. So a = 8 and a^2 = 64; b = 3 and b^2 = 9. Our formula then is