Hello!
As you can see, we have a radius of 6. If we divide, this means that this is 2.5 radians. To convert radians to degrees we use the formula below.

First of all we divide 180 by pi.
180/

≈57.3
Now we multiply by 2.5
57.3(2.5)=143.25°
Note that the angle we see is obtuse, or greater than 90°.
Therefore, ∠
θ≈143.25°
Now we need to convert this back into radians. This can be represented by the equation below.
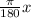
First we divide pi by 180 then multiply by our angle.
 /180(143.25)≈2.5
/180(143.25)≈2.5
Therefore, our angle theta is about 2.5 radians.
I hope this helps!