Hi there!
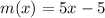
First replace m(x) by y.
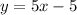
To find the inverse function we must switch the places from the variables x and y.
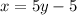
Now we need to isolate the y again to find the formula of the inverse function. First add 5 to both sides.
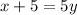
Switch sides.
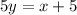
And finally divide both sides by 5.
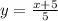
And therefore we can conclude the following:
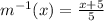
The answer is C.
~ Hope this helps you!