Question

A charge of 8.4 × 10–4 C moves at an angle of 35° to a magnetic field that has a field strength of 6.7 × 10–3 T. If the magnetic force is 3.5 × 10–2 N, how fast is the charge moving?

Answer 1

D. 1.1 x 10^4 m/s

Step-by-step explanation:

just took the exam

Answer 2

The charge is moving with the velocity of
`1.1*10^(4)\ m/s`.

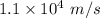Step-by-step explanation:

Given that,

Charge
`q =8.4*10^(-4)\ C`

Angle = 35°

Magnetic field strength
`B=6.7*10^(-3)\ T`

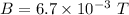
Magnetic force
`F=3.5*10^(-2)\ N`

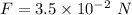
We need to calculate the velocity.

The Lorentz force exerted by the magnetic field on a moving charge.

The magnetic force is defined as:

`F = qvB\sin\theta`

`v = (F)/(qB\sin\theta)`

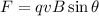
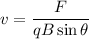
Where,

F = Magnetic force

q = charge

B = Magnetic field strength

v = velocity

Put the value into the formula

`v =(3.5*10^(-2))/(8.4*10^(-4)*6.7*10^(-3)*\sin35^(\circ))`

`v =(3.5*10^(-2))/(8.4*10^(-4)*6.7*10^(-3)*0.57)`

`v = 10910.36\ m/s`

`v = 1.1*10^(4)\ m/s`

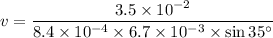
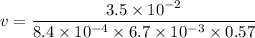
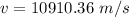
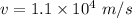
Hence, The charge is moving with the velocity of
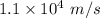`1.1*10^(4)\ m/s`.