Question

I really need the answer now!! Thanks !

Tomas’s math class held a raffle. The student who picked the ticket with a pair of equivalent equations on it would win. Which is the winning ticket?

Answer 1

The winning ticket is: A.
`x^2-3xy+4-2x^2=-x^2-2xy-xy+4`.

Explanation:

We have been given that Tomas’s math class held a raffle. The student who picked the ticket with a pair of equivalent equations on it would win.

Let us check our given pairs of equations one by one.

A.
`x^2-3xy+4-2x^2=-x^2-2xy-xy+4`

Let us combine like terms on the both sides of our equation.

`(x^2-2x^2)-3xy+4=-x^2-(2xy+xy)+4`

`(-x^2)-3xy+4=-x^2-(3xy)+4`

`-x^2-3xy+4=-x^2-3xy+4`

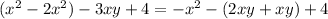
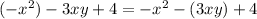
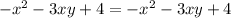
We can see that both sides of our equation are equal, therefore, option A is the correct choice.

B.
`7y^2-yz+4-2yz=7y^2-2yz+4yz`

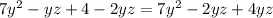
Let us combine like terms on the both sides of our equation.

`7y^2-(yz+2yz)+4=7y^2-(2yz-4yz)`

`7y^2-(3yz)+4=7y^2-(-2yz)`

`7y^2-3yz+4\\eq 7y^2+2yz`

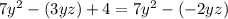
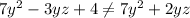
Since the both sides of our equation are not equal, therefore, option B is not a correct choice.

C.
`3a^2-ab+3-3ab=6a^2-2ab+3-2ab`

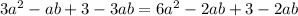
Upon combining like terms we will get,

`3a^2-(ab+3ab)+3=6a^2-(2ab+2ab)+3`

`3a^2-(4ab)+3=6a^2-(4ab)+3`

`3a^2-4ab+3\\eq 6a^2-4ab+3`

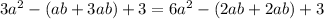
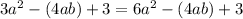
Since the both sides of our equation are not equal, therefore, option C is not a correct choice.

D.
`9s^2-st+5-3st=6s^2-3st+5+3s^2`

Upon combining like terms we will get,

`9s^2-(st+3st)+5=(6s^2+3s^2)-3st+5`

`9s^2-(4st)+5=(9s^2)-3st+5`

`9s^2-4st+5\\eq 9s^2-3st+5`

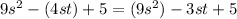
Since the both sides of our equation are not equal, therefore, option D is not a correct choice.

Answer 2

When you collect terms, for the first one you get
-x² -3xy +4 = -x² -3xy +4 . . . . . . equivalent equations.