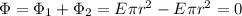Question

A closed cylinder with a 0.15-m radius ends is in a uniform electric field of 300 n/c, perpendicular to the ends. the total flux through the cylinder is:

Answer 1

The total flux through the cylinder is zero.

In fact, the electric flux through a surface (for a uniform electric field) is given by:

`\Phi = E A \cos \theta`

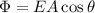
where

E is the intensity of the electric field

A is the surface

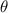`\theta` is the angle between the direction of E and the perpendicular to the surface, whose direction is always outwards of the surface.

We can ignore the lateral surface of the cylinder, since the electric field is parallel to it, therefore the flux through the lateral surface of the cylinder is zero (because
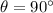`\theta=90^(\circ)` and
`\cos \theta=0`).

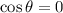On the other two surfaces, the flux is equal and with opposite sign. In fact, on the first surface the flux will be

`\Phi_1 = E \pi r^2`

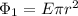
where r is the radius, and where we have taken
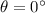`\theta=0^(\circ)` since the perpendicular to the surface is parallel to the direction of the electric field, so
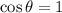`\cos \theta=1`. On the second surface, however, the perpendicular to the surface is opposite to the electric field, so
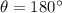`\theta=180^(\circ)` and
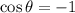`\cos \theta=-1`, therefore the flux is

`\Phi_2 = -E \pi r^2`

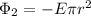
And the net flux through the cylinder is

`\Phi = \Phi_1 + \Phi_2 = E \pi r^2 - E \pi r^2=0`