Question

Identify and equation in point slope form for the line perpendicular to y=1/4x-7 that passes through (-2,-6)

Answer 1

the answer should be B

Answer 2

For this case, we have:

`y-yo = m (x-xo)`
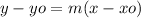
Where,
m: slope of the linear function
(xo, yo): ordered pair that belongs to the linear function.
Since the lines are perpendicular, then the slope is given by:

`m = - (1)/((1)/(4))`
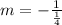
Rewriting we have:

`m = -4`
The line passes through the point (-2, -6), therefore we have:

`(xo, yo) = (-2, -6)`
Substituting values we have:

`y - (- 6) = - 4 (x - (- 2))`
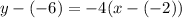
Rewriting we have:

`y + 6 = -4 (x + 2)`
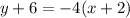Answer:
An equation of the line that passes through the point (-2, -6) with slope -4 is:

`y + 6 = -4 (x + 2)`
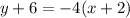option B