Question

Which of the following describes the transformations of g(x)=-(2)^X+4-2 from the parent function ? shift 4 units left, reflect over the x-axis, shift 2 units downshift 4 units left, reflect over the y-axis, shift 2 units downshift 4 units right, reflect over the x-axis, shift 2 units downshift 4 units right, reflect over the y-axis, shift 2 units down

Answer 1

The negative before the 2 reflects over the x axis, The +4 shifts the graph 4 units left and the final - 2 shifts it 2 units down.
Its the first choice.

Answer 2

The correct option is A) shift 4 units left, reflect over the x-axis, shift 2 units down.

Explanation:

Consider the provided information

The parent function for the provided function is
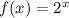`f(x)=2^x` and we need to find the transformations that gives
`g(x)=-(2)^(x+4)-2` from the parent function.

The rules for transformation are:

`f(x)+c` Graph shifted upwards by c units.

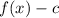`f(x)-c` Graph shifted downwards by c units.

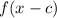`f(x-c)` Graph shifted to right by c units.

`f(x+c)` Graph shifted to left by c units.

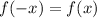`f(-x)=f(x)` Graph reflected across y-axis.

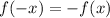`f(-x)=-f(x)` Graph reflected across x-axis.

Now consider the given function
`g(x)=-(2)^(x+4)-2` replace x with -x
`g(x)=-(2)^(-x+4)-2`

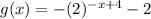
which shows the function reflected across x-axis.

Now observe the parents function and provided function f(x) and g(x),we can observe the transformations:

The parent function
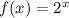`f(x)=2^x` is shifted to left by 4 units. From the above rule.

The parent function
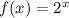`f(x)=2^x` is shifted downwards by 2 units. Because of -2

Hence, the correct option is A) shift 4 units left, reflect over the x-axis, shift 2 units down.