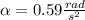Question

You accelerate your car from rest at a constant rate down a straight road, and reach 22.0 m/s in 117 s. the tires on your car have radius 0.320 m. assuming the tires rotate in a counterclockwise direction, what is the angular acceleration of the tires?

Answer 1

For this case, the first thing to do is find the linear acceleration of the car.

We have then:

`image`

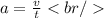
Where,

v: speed

t: time

Substituting values we have:

`image`

`image`

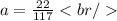
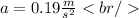
We are now looking for angular acceleration.

For this, we use the following equation:

`\alpha =(a)/(r)`

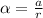
Where,

a: linear acceleration

r: radius of the tires

Substituting values we have:

`image`

`\alpha = 0.59 (rad)/(s^2)`

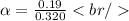
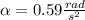
Answer:

The angular acceleration of the tires is:

`\alpha = 0.59 (rad)/(s^2)`