Question

A car enters a horizontal, curved roadbed of radius 50 m. the coefficient of static friction between the tires and the roadbed is 0.20. what is the maximum speed with which the car can safely negotiate the unbanked curve?

Answer 1

Maximum speed, v = 9.89 m/s

Step-by-step explanation:

It is given that,

Radius of the curve, r = 50 m

The coefficient of static friction between the tires and the roadbed is 0.20,
`\mu=0.2`

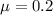
To find,

The maximum speed with which the car can safely negotiate the unbanked curve.

Solution,

The net force acting on the car is balanced by its centripetal force such that the maximum speed of the car is given by :

`v=√(\mu rg)`

`v=√(0.2* 50* 9.8)`

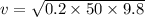
v = 9.89 m/s

So, the maximum speed with which the car can safely negotiate the unbanked curve is 9.89 m/s.

Answer 2

Previous results tell us the speed (v) is given in terms of the coefficient of friction (k) and the radius of the curve (r) as
v = √(kgr)
v = √(0.20·9.8 m/s²·50 m)
= 7√2 m/s ≈ 9.90 m/s