A perfect square must be hidden within all of those radicands in order to simplify them down to what the answer is.
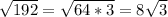
.
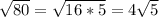
.
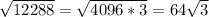
. The rules for adding radicals is that the index has to be the same (all of our indexes are 2 since we have square roots), and the radicands have to be the same. In other words, we cannot add the square root of 4 to the square root of 5. They either both have to be 4 or they both have to be 5. So here's what we have thus far:
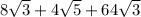
. We can add
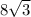
and
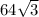
to get
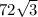
. That means as far as our answer goes, A = 72 and B = 4, or (72, 4), choice a.