Question

Sec 11pi/3

Use the fact that there are 2pi radians in each circle to find another angle, smaller than 2pi, that is equivalent to 11pi/3.

Answer 1

I prefer the word "coterminal" to equivalent; coterminal angles have all the same values for their trig functions. They differ by
`2\pi k, \quad` integer
`k`.


`\sec (11 \pi)/(3) = \sec\left( ( 11 \pi)/(3) - 4\pi \right) = \sec\left( ( 11 \pi)/(3) - 4\pi \right) = \sec\left( ( 11 \pi)/(3) - (12\pi)/(3) \right)`


`= \sec\left(-(\pi)/(3)\right) = (1)/(\cos(-(\pi)/(3))) = (1)/(\cos \frac \pi 3)= (1)/(\frac 1 2) = 2`

Answer 2

`sec(11\pi )/(3) =2`

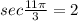
Explanation:

Given

`sec(11\pi )/(3)`

=
`sec( 4\pi -(\pi )/(3))`

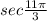
It lies in the IV quadrant .Therefore we can write as

`sec(11\pi )/(3) =sec(\pi )/(3)`

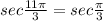
Because
`sec(2\pi -\theta)= sec\theta`

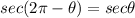
Because
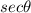`sec\theta` is positive in first quadrant and IV quadrant . There is
`\theta` lies in the IV quadrant .

Hence,
`sec(\pi )/(3)` is positive in IV quadrant .

`sec(11\pi )/(3) =sec(\pi )/(3)`

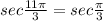
We know that value of
`sec(\pi )/(3) =sec60^(\circ)=2`

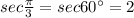
Therefore,
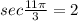`sec(11\pi )/(3) =2`.