Question

In the diagram below, BC is an altitude of ABD. To the nearest whole unit, what is the length of CD?

Answer 1

First we need to calculate the 2 angles that make up Angle B at the top of the triangle.
Using that angle we can find the length of CD.


See the attached picture:

Answer 2

D. 26.

Explanation:

We have been given an image of a triangle. We are asked to find the length of CD.

We will use altitude on hypotenuse theorem to solve our given problem.

`\frac{CD}{\text{Altitude}}=\frac{\text{Altitude}}{AC}`

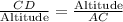
Upon substituting our given values, we will get:

`(CD)/(37)=(37)/(53)`

`(CD)/(37)* 37=(37)/(53)* 37`

`CD=(37* 37)/(53)`

`CD=(1369)/(53)`

`CD=25.830188679\approx 26`

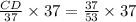
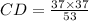
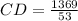
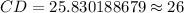
Therefore, the length of CD is 26 units and option D is the correct choice.