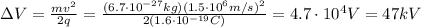2 Answers

Riggy · Answer 1 · 2019-10-25T14:17:21+0000

We can solve the problem by using conservation of energy.

In fact, the electric potential energy lost by the charge when moving through the potential difference is equal to the kinetic energy acquired:

$\Delta U=\Delta K =K_f -K_i =K_f$

where
K_f is the final kinetic energy, and
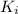K_i is the initial kinetic energy, which is zero since the particle starts from rest.

We can rewrite the equation above as:

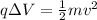
$q \Delta V=(1)/(2)mv^2$

where

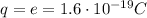$q=e=1.6 \cdot 10^(-19)C$ is the charge of the ion

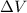$\Delta V$ is the potential difference

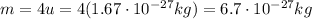$m=4u=4 (1.67 \cdot 10^(-27) kg)=6.7 \cdot 10^(-27) kg$ is the mass of the ion

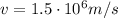$v=1.5 \cdot 10^6 m/s$ is the final speed of the ion

Substituting the numbers and rearranging the equation, we can find the potential difference needed:

$\Delta V=(mv^2)/(2q)=((6.7 \cdot 10^(-27)kg)(1.5 \cdot 10^6 m/s)^2)/(2(1.6 \cdot 10^(-19)C))=4.7 \cdot 10^4 V=47 kV$

Please log in or register to add a comment.