Let
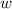
be the speed of the westbound train,

eastbound
Westbound is 10mph faster than eastbound:
w = 10 + e
After two hours, they're 400 miles apart:
400 = 2w + 2e
Solving,
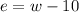
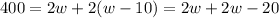
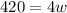
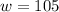
mph
That's the answer. That means the eastbound train is going 95 mph, so they're separating at 200 mph, so 400 miles apart after two hours. Check.