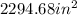Question

A regular octagon has side length 10.9 in. The perimeter of the octagon is 87.2 in cm and the area is 573.67 in2. A second octagon has side lengths equal to 21.8 in. Find the area of the second octagon. Round to the nearest hundredth

Answer 1

To solve this problem you must apply the proccedure shown below:

1. If the first octagon and the second octagon are similar, you need to find the ratio of the lengths, as below:

`ratio=21.8in/10.9in\\ ratio=2`

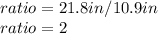
2. The ratio of the area is:

`ratio=2^(2) =4`

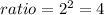
4. Then, you must multiply the ratio by the area of the first octagon to calculate the second area:

`A2=4A1\\ A2=4(573.67in)\\ A2=2294.68in^(2)`

The answer is:
`2294.68in^(2)`