Question

Problem A
Please help me

Answer 1

By the Zero Product Property, either
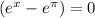
`( e^(x)- e^( \pi ) )=0` or
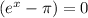
`(e^(x)- \pi )=0`. So we will solve for x in each case. We need to take the natural log of each side in both cases since x is an exponent to base e, and the natural log has a base of e. So taking the natural log of e "undo" each other, leaving us with just x. Like this:
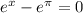
`e^(x)-e^ \pi =0` so
`e^x=e^ \pi`. Taking the natural log of each side gives us
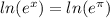
`ln(e^x)=ln(e^ \pi )`. Again, taking the natural log of base e undo each other, so
`x= \pi`. That's the first root. In the second case,
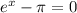
`e^x- \pi =0` so
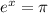
`e^x= \pi`. Taking the natural log of both sides we get
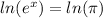
`ln(e^x)=ln( \pi )`. That means that
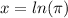
`x=ln( \pi )`. Your solutions are
`x = \pi ,ln( \pi )`